Java二叉搜索树遍历操作详解【前序、中序、后序、层次、广度优先遍历】

本文实例讲述了Java二叉搜索树遍历操作。分享给大家供大家参考，具体如下：

前言：在上一节Java二叉搜索树基础中，我们对树及其相关知识做了了解，对二叉搜索树做了基本的实现，下面我们继续完善我们的二叉搜索树。

对于二叉树，有深度遍历和广度遍历，深度遍历有前序、中序以及后序三种遍历方法，广度遍历即我们寻常所说的层次遍历，如图：

因为树的定义本身就是递归定义，所以对于前序、中序以及后序这三种遍历我们使用递归的方法实现，而对于广度优先遍历需要选择其他数据结构实现，本例中我们使用队列来实现广度优先遍历。

四种基本的遍历思想为：

前序遍历：根结点 ---> 左子树 ---> 右子树中序遍历：左子树---> 根结点 ---> 右子树后序遍历：左子树 ---> 右子树 ---> 根结点层次遍历：从上到下，从左到右。

比如，以下二叉树的各种遍历：

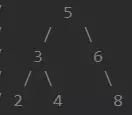
前序遍历:5-3-2-4-6-8中序遍历:2-3-4-5-6-8后序遍历:2-4-3-8-6-5层次遍历：5-3-6-2-4-8

依据上文提到的遍历思路：根结点 ---> 左子树 ---> 右子树，代码实现如下：

//二分搜索树的前序遍历(前序遍历：根结点 ---> 左子树 ---> 右子树) public void preOrder() { preOrder(root); } //前序遍历以node为根的二分搜索树,递归算法 private void preOrder(Node node) { if (node == null) { return; } System.out.println(node.e); preOrder(node.left); preOrder(node.right); }二、中序遍历

依据上文提到的遍历思路：左子树 ---> 根结点 ---> 右子树，代码实现如下：

//二分搜索树的中序遍历(中序遍历：左子树---> 根结点 ---> 右子树) public void inOrder() { inOrder(root); } //中序遍历以node为根的二分搜索树,递归算法 private void inOrder(Node node) { if (node == null) { return; } inOrder(node.left); System.out.println(node.e); inOrder(node.right); }三、后序遍历

依据上文提到的遍历思路：左子树 ---> 右子树 ---> 根结点,代码实现如下：

//二分搜索树的后序遍历(后序遍历：左子树 ---> 右子树 ---> 根结点) public void postOrder() { postOrder(root); } //后序遍历以node为根的二分搜索树,递归算法 private void postOrder(Node node) { if (node == null) { return; } postOrder(node.left); postOrder(node.right); System.out.println(node.e); }四、层次遍历

对于层次遍历，我们基于队列来实现，思路如下：（1）先在队列中增加根结点（2）对于随意其余任意节点，在其出队列的时候访问（假设左孩子和右孩子有不为空的情况，入队列）代码实现如下：

//层次遍历--(基于队列实现) public void levelOrder() { Queue<Node> q = new LinkedList<>(); q.add(root); while (!q.isEmpty()) { Node cur = q.remove(); System.out.println(cur.e); if (cur.left != null) {q.add(cur.left); } if (cur.right!=null){q.add(cur.right); } } }

源代码地址 https://github.com/FelixBin/dataStructure/blob/master/src/BST/BST.java

更多关于java算法相关内容感兴趣的读者可查看本站专题：《Java数据结构与算法教程》、《Java操作DOM节点技巧总结》、《Java文件与目录操作技巧汇总》和《Java缓存操作技巧汇总》

希望本文所述对大家java程序设计有所帮助。